مفاهیم پایه در آمار زیستی (بخش دوم، آزمون ها)

در این بخش از مقاله راجع به آزمون‌های مختلف در آمار زیستی و مثال های ساده آن در نرم افزار زبان برنامه‌نویسی R و رابط گرافیگی RStudio پرداخته شده است.

 آزمون های نیکویی برازش

از این آزمون ها برای بررسی پیروی داده ها از یک توزیع خاص استفاده می شود. هدف ما از انجام این آزمون بررسی نرمال بودن داده ها و نهایتا انتخاب آزمون صحیح است. از جمله معروف ترین آزمون های نیکویی برازش می توان به کلموگروف اسمیرنوف اشاره کرد.

دستور انجام این آزمون در نرم افزار زبان برنامه‌نویسی R و رابط گرافیگی RStudio به صورت:

Ks.test (mydata,”proposed distribution”)

آزمون های پارامتری

اگر توزیع داده های مورد بررسی نرمال باشد برای بررسی فرضیات مورد نظر از آزمون های پارامتری استفاده می‌کنیم.

آزمون های پارامتری مرتبط با بررسی میانگین

• آزمون t تک نمونه ای
• آزمون t دو نمونه ای مستقل
• آزمون t دو نمونه وابسته (زوجی)
• آزمون بررسی میانگین چند گروه مستقل (آنالیز واریانس یک طرفه و دو طرفه)

آزمون t تک نمونه ای

آزمون t تک نمونه ای که ساده ترین نوع آزمون های t است جهت تعیین این که آیا میانگین مشاهده شده در نمونه که به صورت تصادفی از جامعه انتخاب شده است، مقداری برابر با میانگین مفروض جامعه دارد یا خیر، به کار می رود.

دستور انجام این آزمون در نرم افزار زبان برنامه‌نویسی R و رابط گرافیگی RStudio به صورت

t.test(mysample, mu=a, alt=”g, l, two”)

آزمون t دو نمونه ای مستقل

اگر خواهان مقایسه میانگین دو گروه مستقل که هر کدام دارای توزیع نرمال هستند باشیم آزمون مورداستفاده t دو نمونه ای مستقل است. مانند زمانی که می خواهیم میانگین وزن دو گروه زنان و مردان را مقایسه کنیم.

دستور انجام این آزمون در نرم افزار زبان برنامه‌نویسی R و رابط گرافیگی RStudio به صورت

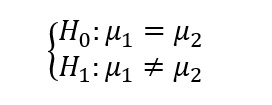
t.test (x,y)

آزمون دو نمونه وابسته

برای مقایسه میانگین دو گروه وابسته که دارای توزیع نرمال هستند از این آزمون مقایسه می کنیم. در واقع این آزمون برای داده های مناسب است که هر نمونه یا گروه در دو وضعیت متفاوت (زمانی یا مکانی) اندازه گیری شده باشند. هدف از این آزمون تعیین اثرگذاری یک رخ داد بر افراد حاضر در گروه است.

دستور انجام این آزمون در نرم افزار زبان برنامه‌نویسی R و رابط گرافیگی RStudio به صورت

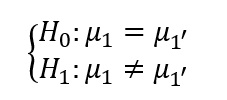
t.test (x,y,paired=TRUE)

مقایسه میانگین چند گروه (بیش از دو گروه)

برای مقایسه میانگین چند گروه از آنالیز واریانس (ANOVA) استفاده می کنیم. آناليز واريانس يك شيوه آماری كارآمد برای مقايسه ميانگين يك صفت كمی در سطوح يك متغير کیفی است. فرضیات مورد نیاز در این آزمون عبارتند از:

• نرمال بودن مشاهدات هرگروه
• ثابت بودن واریانس ها در گروه ها
• مستقل بودن خطاها

به عنوان مثال در آنالیز واریانس یک طرفه (یک متغیر کمی و یک متغیر کیفی داریم) وقتی می خواهیم سه روش آموزش رياضيات را در يك آموزشكده با هم مقايسه كنيم. بايد ميانگين نمرات سه گروه از دانشجويان را كه هر گروه با يك روش مختلف تدريس شده اند، با هم مقايسه شوند. در اين جا به متغير روش آموزش، متغير فاكتور يا متغير مستقل می گويند. اين متغير در اين مثال شامل سه سطح است. امكان دستكاری سطوح متغير مستقل در آناليز واريانس وجود دارد.

دستور انجام این آزمون در نرم افزار زبان برنامه‌نویسی R و رابط گرافیگی RStudio به صورت:

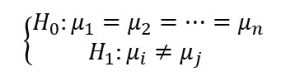
aov(x~y,data=mydata)

آنالیز واریانس دو طرفه

این آزمون نیز مشابه حالت قبلی برای مقایسه میانگین یک متغیر کمی با توجه به دو متغیر کیفی تهیه شده است. فرض صفر این آزمون به صورت:

مثال: فرض کنیم از کلیه دانشجویان پسرو دختری که در درس آمار مقدماتی ثبت نام کرده اند، نمونه هایی به صورت تصادفی انتخاب کرده ایم و یک امتحان درباره آمار مقدماتی از آنها به عمل آورده ایم.

علاوه بر این، به نیمی از دانشجویان پسر و هم چنین به نیمی از دانشجویان دختر در هنگام تدریس راهنماییهایی درباره چگونگی مطالعه تدریس شده است و نیمه های دیگر دو گروه راهنمایی نشدند.

تحلیل واریانس دو طرفه به ما امکان می دهد که به برخی از سوالات مربوط به عملکرد دانشجویان در امتحان آمار پاسخ دهیم.

به عنوان مثال، آیا بین نمره های دانشجویان پسر و دختر تفاوت معناداری وجود دارد؟

• آیا راهنمایی دانشجویان هنگام تدریس، تاثیری در نمره امتحانی انها داشته است؟
• آیا بین جنس دانشجویان و راهنمایی آنها کنش متقابل وجود دارد؟
• یا به عبارت دیگر، نمره های دانشجویان دختری که راهنمایی نشده اند بهتر از نمره های دانشجویان دختری است که هنگام تدریس راهنمایی شده اند؟

دستور انجام این آزمون در نرم افزار زبان برنامه‌نویسی R و رابط گرافیگی RStudio به صورت:

aov(x~group1*group2,data=mydata)

آزمون های تعقیبی

با رد شدن فرض صفر در آنالیز واریانس (نتیجتا عدم برابری واریانس گروه ها) محقق به دنبال یافتن گروهی است که میانگین آن با سایر گروه ها متفاوت است. برای این کار از آزمون های تعقیبی استفاده می کنیم. برخی از این ازمون ها عبارتند از توکی، شفه و…

دستور انجام این آزمون در نرم افزار زبان برنامه‌نویسی R و رابط گرافیگی RStudio به صورت:

tukeyHSD(mymodel2, which = “mygroup”)

طرح اندازه های تکراری

برای مقایسه میانگین چند گروه (بیش از دو گروه) وابسته از این آزمون استفاده می کنیم.  در واقع این طرح حالت تعمیم یافته آزمون t زوجی است. برای مثال میانگین فروش شرکتی طی چهار سال اخیر و یا میزان اثرگذاری یک دارو در یک دوره شش ماه از این نوع مطالعه هستند.

آزمون های ناپارامتری

اگر توزیع داده‌های مورد بررسی نرمال نباشد نمی توان از آزمون های ناپارامتری استفاده کرد. بنابراین آزمون ها ناپارامتری بخش مهمی از آزمون های مورد بررسی هستند.

آزمون علامت تک نمونه: برای آزمون فرض پیرامون میانگین یک جامعه استفاده می شود.

آزمون علامت زوجی: برای آزمون فرض پیرامون دو میانگین از یک جامعه استفاده می شود.

ویلکاکسون: همان آزمون علامت زوجی است که در آن اختلاف نسبی تفاوت از میانگین لحاظ می شود.

مان-ویتنی: به آزمون U نیز موسوم است و جهت مقایسه میانگین دو جامعه استفاده می شود.

کروسکال-والیس: از این آزمون به منظور بررسی اختلاف میانگین چند جامعه آماری استفاده می شود. به آزمون H نیز موسوم است و تعمیم آزمون U مان-ویتنی می باشد. آزمون کروسکال-والیس معادل روش پارامتریک آنالیز واریانس تک عاملی است.

فریدمن: این آزمون معادل روش پارامتریک آنالیز واریانس دو عاملی است که در آن k تیمار به صورت تصادفی به n بلوک تخصیص داده شده اند.

آزمون تقارن توزیع: در این آزمون شکل توزیع مورد سوال قرار می گیرد. فرض بدیل آن است که توزیع متقارن نیست.

آزمون میانه: جهت مقایسه میانه دو جامعه استفاده می شود و برای k جامعه نیز قابل تعمیم است.

مک نمار: برای بررسی مشاهدات زوجی درباره متغیرهای دو ارزشی استفاده می شود.

آزمون Q کوکران: تعمیم آزمون مک نمار در k نمونه وابسته است.

ضریب همبستگی اسپیرمن: برای محاسبه همبستگی دو مجموعه داده که به صورت ترتیبی قرار دارند استفاده می شود.

آزمون من ویتنی

آزمون من–ويتنی يك آزمون مقايسه ای برای مقايسه وضعيت دو گروه مستقل است و وقتی داده های يك مطالعه به صورت كيفی ترتيبی باشند (نرمال نباشند) بهتر است از اين آزمون كه يك آزمون ناپارامتری پارامتری و معادل آزمون دو نمونه مستقل t است، استفاده كرد.

به این آزمون، آزمون جمعی رتبه ای ویلکاکسون نیز گفته می شود.

دستور انجام این آزمون در نرم افزار زبان برنامه‌نویسی R و رابط گرافیگی RStudio به صورت:

wilcox.test(x~y)

 آزمون ویلکاکسون (رتبه علامت دار)

آزمون رتبه ای علامت دار ویلکاکسون یک آزمون برای فروض آماری ناپارامتری است که به هنگام مقایسه دو نمونه جفتی و مرتبط کاربرد دارد. همچنین از این آزمون برای تشخیص تفاوت میانگین یک نمونه در اندازه های مکرر استفاده می شود. این آزمون جایگزین مناسبی برای آزمون تی استودنت جفتی هنگامی که جامعه دارای توزیع نرمال نمی باشد است.

دستور انجام این آزمون در نرم افزار زبان برنامه‌نویسی R و رابط گرافیگی RStudio به صورت:

wilcox.test(x,y, paired=TRUE)##dependent group

آزمون کراسکال والیس

برای مقایسه میانگین چند گروه مستقل وقتی که توزیع مشاهدات در گروه ها نرمال نباشد. این آزمون معادل ناپارامتری آنالیز واریانس یک طرفه است.  برای مقايسه های سه و بيشتر از سه گروه استفاده می كنيم. روش كروسكال- واليس اين فرضيه را كه k  گروه نمونه از يك جامعه آماری مشترك يا جامعه آماری شبيه به هم كه با توجه به ميانگين ها استخراج شده اند، آزمون می كند.

فرضیه‌های مورد آزمون به صورت:

است. فرضیات این آزمون عبارتند از یکسان بودن توزیع گروه ها، مستقل بودن گروه ها و تصادفی بودن نمونه های جمع آوری شده است.

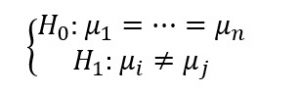
دستور انجام این آزمون در نرم افزار زبان برنامه‌نویسی R و رابط گرافیگی RStudio به صورت:

kruskal.test(Ozone ~ Month, data = airquality)

آزمون فریدمن

این آزمون معادل طرح اندازه های تکراری در حالت پارامتری است. آزمون فریدمن یک آزمون ناپارامتری است که برای مقایسه سه یا بیش از سه گروه وابسته که حداقل در سطح رتبه ای اندازه گیری می شوند، مورد استفاده قرار می گیرد. این آزمون می تواند در مورد داده های پیوسته (فاصله ای یا نسبی) نیز به کاربرده شود، اما در هنگام محاسبه این داده ها نیز رتبه بندی آن ها مدنظر قرار می گیرد.

آزمون نسبت

از این آزمون برای بررسی برابری نسبت وجود یک صفت در جامعه استفاده می کنیم. به عنوان مثال پزشکی ادعا می‌کند که برای یک بیماری خاص، روش درمان بهتری دارد. زیرا از ده بیماری که معالجه کرده است 7 نفر آن ها بهبود پیدا کرده‌اند. در صورتی که درمان هائی که تاکنون صورت گرفته بیشتر از 50% موفقیت نداشته است. سئوال این است که آیا واقعاً روش درمانی ادعا شده پزشک بهتر از روش‌های قبل است؟ برای پاسخ دادن به این پرسش که آیا نسبت موفقیت در یک آزمایش دو حالتی با یک مقدار خاص برابری دارد یا نه؟ از آزمون دو جمله‌ای استفاده می‌كنيم.

می توان از این آزمون برای مقایسه میزان نسبت ها در دو جامعه نیز استفاده کرد.

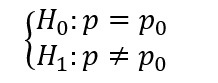
دستور انجام این آزمون در نرم افزار زبان برنامه‌نویسی R و رابط گرافیگی RStudio به صورت:

prop.test(x,n,p)

آزمون کای‌دو

برای بررسی وجود ارتباط بین متغیرهای کیفی باید از جداول توافقی و آزمون کای دو استفاده کرد. متغیرهای مورد استفاده در این آزمون کیفی هستند. به عنوان مثال بررسی وجود ارتباط بین مصرف سیگار و جنسیت.

 ضریب همبستگی

با استفاده از ضریب همبستگی می توان میزان رابطه خطی و جهت آن را بین دو متغیر کمی بررسی کرد. مقدار این صفت بین 1- تا 1 تغییر می کند. هرچه به یک نزدیک تر یعنی همبستگی دو متغیر بیشتر و در جهت مثبت می باشد. سه نوع ضریب همبستگی داریم که عبارتند از پیرسون، اسپیرمن و کندال معروف ترین ضریب همبستگی موجود پیرسون است. اگر ضریب همبستگی صفر باشد یعنی رابطه خطی بین دو متغیر وجود ندارد. برای بررسی صفر بودن ضریب همبستگی آزمون زیر را داریم:

دستور انجام این آزمون در نرم افزار زبان برنامه‌نویسی R و رابط گرافیگی RStudio به صورت:

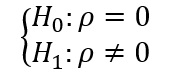
Cor(x,y)
Cor.test(x,y)

رگرسیون خطی

برای بررسی اثر گذاری چند (یک) متغیر مستقل بر روی یک (چند) متغیر وابسته از رگرسیون استفاده می کنیم. رگرسیون انواع مختلف خطی و غیر خطی دارد که با توجه به نوع مساله باید انتخاب شوند. در رگرسیون خطی معمولی متغیرهای مستقل و وابسته هر دو کمی هستند. پس از برازش خط رگرسیون به ازای هر متغیر موجود یک ضریب رگرسیونی بدست می آید که می توان آن را نیز آزمون کرد.

پس از انجام آزمون فرض فوق می توان متغیرهایی که ضرایب آنها صفر شده اند را می توان حذف کرد.

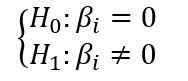
دستور انجام این آزمون در نرم افزار زبان برنامه‌نویسی R و رابط گرافیگی RStudio به صورت:

lm(y~ x)

برخی از فرضیات که برقراری آنها برای اعتماد به نتایج مدل رگرسیونی اهمیت دارند عبارت اند از:

• ثبات در واریانس باقی مانده ها
• توزیع باقی مانده ها نرمال باشد
• وجود رابطه خطی بین متغیرهای مستقل و وابسته
• استقلال باقی مانده ها

 رگرسیون لجستیک

اگر متغیر پاسخ مورد نظر ما یک متغیر کیفی (گسسته مقدار) باشد نمی توان از رگرسیون خطی معمولی استفاده کرد در این حالت باید از رگرسیون لجستیک استفاده کنیم. متداول ترین حالت استفاده از رگرسیون لجستیک برای متغیرهای وابسته دودویی است.

برخلاف رگرسیون خطی معمولی تنها فرض موجود در این رگرسیون استقلال مشاهدات است.

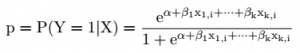
دستور انجام این آزمون در نرم افزار زبان برنامه‌نویسی R و رابط گرافیگی RStudio به صورت:

glm(y~x, family=binomial)

 تحلیل بقا

بررسی رکوردها تا زمان رخ دادن یک اتفاق و بررسی تاثیر گذاری سایر متغیرها بر روی اتفاق رخ داده را تحلیل بقا نامند. در واقع متغیر مورد نظر ما در تحلیل بقا زمان رخ داد است. سازگاری این مدل با داده‌های سانسور شده بسیار با اهمیت است.

از طرفی مقایسه میزان بقا در گروه های مختلف را می توان به راحتی با استفاده از آزمون های موجود انجام داد. آزمون مورد استفاده برای مقایسه گروه های مختلف آزمون لگاریتم رتبه ای است.

دستور انجام این آزمون در نرم افزار زبان برنامه‌نویسی R و رابط گرافیگی RStudio به صورت:

survfit(Surv(days,status)~1)##kaplan mier
survdiff(Surv(days,status==1)~sex)##log rank test

خدمات گروه علمی بامازیست

جهت هرگونه مشاوره و راهنمایی در ارتباط با دستورات آزمون‌ها در نرم افزار زبان برنامه‌نویسی R و رابط گرافیگی RStudio می‌توانید از مقالات گروه علمی بامازیست بهره بگیرید.